Powerful p-group

In mathematics, in the field of group theory, especially in the study of p-groups and pro-p-groups, the concept of powerful p-groups plays an important role. They were introduced in (Lubotzky & Mann 1987), where a number of applications are given, including results on Schur multipliers. Powerful p-groups are used in the study of automorphisms of p-groups (Khukhro 1998), the solution of the restricted Burnside problem (Vaughan-Lee 1993), the classification of finite p-groups via the coclass conjectures (Leedham-Green & McKay 2002), and provided an excellent method of understanding analytic pro-p-groups (Dixon et al. 1991).

Formal definition

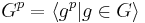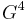A finite p-group $G$ is called powerful if the commutator subgroup $[G,G]$ is contained in the subgroup $G^p = \langle g^p | g\in G\rangle$ for odd $p$ , or if $[G,G]$ is contained in the subgroup $G^4$ for p=2.

Properties of powerful p-groups

Powerful p-groups have many properties similar to abelian groups, and thus provide a good basis for studying p-groups. Every finite p-group can be expressed as a section of a powerful p-group.

Powerful p-groups are also useful in the study of pro-p groups as it provides a simple means for characterising p-adic analytic groups (groups that are manifolds over the p-adic numbers): A finitely generated pro-p group is p-adic analytic if and only if it contains an open normal subgroup that is powerful: this is a special case of a deep result of Michel Lazard (1965).

Some properties similar to abelian p-groups are: if $G$ is a powerful p-group then:

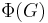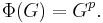
The Frattini subgroup $\Phi(G)$ of $G$ has the property $\Phi(G) = G^p.$
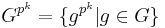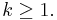$G^{p^k} = \{g^{p^k}|g\in G\}$ for all $k\geq 1.$ That is, the group generated by $p$ th powers is precisely the set of $p$ th powers.
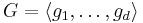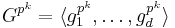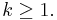
If $G = \langle g_1, \ldots, g_d\rangle$ then $G^{p^k} = \langle g_1^{p^k},\ldots,g_d^{p^k}\rangle$ for all $k\geq 1.$
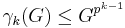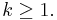
The $k$ th entry of the lower central series of $G$ has the property $\gamma_k(G)\leq G^{p^{k-1}}$ for all $k\geq 1.$
Every quotient group of a powerful p-group is powerful.
The Prüfer rank of $G$ is equal to the minimal number of generators of $G.$

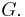
Some less abelian-like properties are: if $G$ is a powerful p-group then:

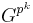$G^{p^k}$ is powerful.
Subgroups of $G$ are not necessarily powerful.

References

Lazard, Michel (1965), Groupes analytiques p-adiques, Publ.Math.IHES 26 (1965), 389-603.
Dixon, J. D.; du Sautoy, M. P. F.; Mann, A.; Segal, D. (1991), Analytic pro-p-groups, Cambridge University Press, ISBN 0-521-39580-1, MR 1152800
Khukhro, E. I. (1998), p-automorphisms of finite p-groups, Cambridge University Press, ISBN 0-521-59717-X, MR 1615819
Leedham-Green, C. R.; McKay, Susan (2002), The structure of groups of prime power order, London Mathematical Society Monographs. New Series, 27, Oxford University Press, ISBN 978-0-19-853548-5, MR 1918951
Lubotzky, Alexander; Mann, Avinoam (1987), "Powerful p-groups. I. Finite Groups", J. Algebra 105 (2): 484–505, doi:10.1016/0021-8693(87)90211-0, MR 0873681
Vaughan-Lee, Michael (1993), The restricted Burnside problem (2nd ed.), Oxford University Press, ISBN 0-19-853786-7, MR 1364414